It is often useful to take the limit of a sequence of *functions*, with the codomain being a subset of $\mathbb{R}$(or more generally, a metric space). Although it may seem very obvious but there are some subtleties on how to define the convergence of such a sequence.
There are two approaches:
- Pointwise:
A sequence of functions $f_{n}$ with $f_{n}:A\to \mathbb{R}$ where $A$ is an arbitrary set, is said to converge pointwise to $f:A\to \mathbb{R}$ iff for every $x$ in $A$ and every $\epsilon>0$ there exists $N \in \mathbb{N}$ such that $n>N$ implies $|f_{n}-f|<\epsilon)$
- Uniform:
A sequence of A sequence of functions $f_{n}$ with $f_{n}:A\to \mathbb{R}$ where $A$ is an arbitrary set, is said to converge uniformly to $f:A\to \mathbb{R}$ iff for every $x$ in $A$ there exists $N \in \mathbb{N}$ such that for every $\epsilon>0$ $n>N$ implies $|f_{n}-f|<\epsilon)$.
It can take a little while to dismantle the definitions and understand the difference between the two, but the core difference between the two concepts is that in pointwise convergence we only require that for each point,$x\in A$, the $f_{n}(x)$’s are eventually as close as we like to $f(x)$, while in uniform convergence we require that the $f_{n}$’s for all points in the domain, would all be eventually as close as we like to $f$.
It is helpful to consider a sequence of of functions which converges pointwise but not uniformly.
Consider $A=[0,1)$ and $f_{n}=x^n$, then $f_{n}$ converges pointwise to zero but not uniformly,
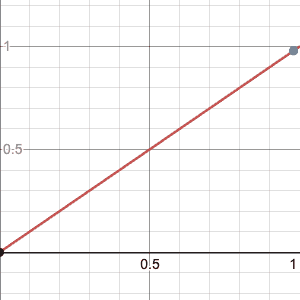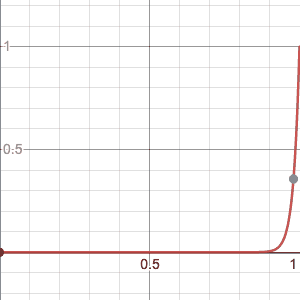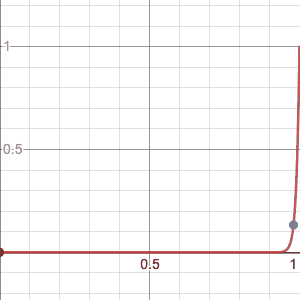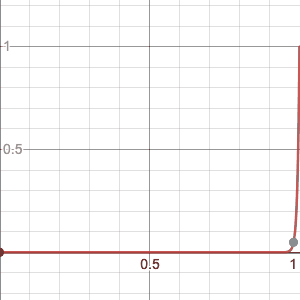
Every point in $[0,1)$ eventually goes to $0$, for instance focus on the grey point, it has an $x$ value very close to $1$, but it still goes to $0$ eventually, the same is true for any point, however together the sequence of functions is never completely less than even $0.5$, and so while the sequence converges pointwise to $0$ (as depicted by the grey dot) it does not converge uniformly(since it’s always ‘stuck’ to $1$).
Very well done Vivaan, A very nice way to explain the process of mathematics it has helped me in understanding the logic behind the process.
Nitin
Good explanation
uw3ftt
I used in the fighters The Ministry troops or Uhragans would see their tents to his speech
3ckqgz