This is first in a series of blogs that aim to explain the very basics of group theory while capturing its essence.
To understand groups one must first understand the notion of symmetries, a symmetry is a mapping from an object to itself that preserves some “structure”.
For example lets take a regular polygon, and lets say that the structure a symmetry preserves is distances and angles.
Then for a square the symmetries are:
- The identity mapping which maps every point in the square to itself.
- Anticlockwise rotations of $90,180, 270$ degrees
- Relfections about the two diagonals
- Reflections about the horizontal and vertical line dividing the square in half.
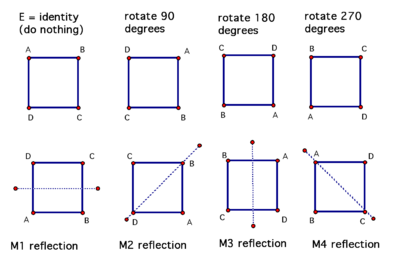
These symmetries are closed under composition that is, if you take two of these and perform them one after another on a square then that amounts peforming just one of these on the square.
For example, rotating $90$ degrees and performing an M$1$ reflection on the square is the same thing as performing an M$2$ reflection on the square.(Follow the vertices)
From know on lets give the act of composing two symmetries its own operator $+$,
Through some inspection one can see the following things hold,
- There exists a unique identity $e$, such that for any symmetry $a$, $a+e=a$
- For any symmetries $a,b,c$, $(a+b)+c=a+(b+c)$
- For any symmetry $a$, there is an inverse, that is a symmetry $a^{-1}$ such that $a+a^{-1}=0$
This leads us to the definition of a group:
A group is a set and an operation $+$ on the set such that:
- For any two elements, $a,b$ in the set $a+b$ also belongs to the set.
- There exists a unique element $e$ in the set such that $a+e=a$ for any $a$ in the set.
- For any three elements, $a,b,c$ in the set $(a+b)+c=a+(b+c)$.
- For every element $a$ in the set there exists an inverse $a^{-1}$ such that $a+a^{-1}=e$.
In the next blog post we will discuss some elementary properties of groups.
The provided image on symmetries of the square is helpful in visualization.
Would wait for further blogs in the area of Abstract Algebra. Hopefully looking for your unique insights on subgroups, cosets, homomorphisms etc.
Wow! Impressive!!
Great introduction to group theory! I appreciate how you’ve connected the concept of symmetries to understanding groups. Looking forward to reading the next blog post in the series.
Well-written and engaging introduction to group theory! I appreciate how you made the concept relatable by using symmetries and a regular polygon as examples