The aim of this blogpost is to prove that given $n$ points with distinct $x$ coordinates there is a unique polynomial function passing through all of them. Basically this polynomial is the (unique) polynomial of lowest degree that ‘fits’ given data. This theroem is known as the ‘Lagrange interpolation theorem’ in numerical analysis.
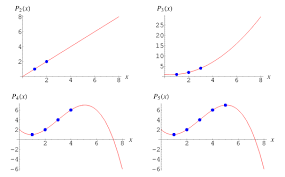
From hence forth by a set of $n$-coordinate pairs we refer to a set indexed by $0,1,\cdots,n-1$, such that the $x$-coordinates of all tuples in the set are distinct. It is well know that given a set of $2$-coordinate pairs one can find a unique linear function(a degree one polynomial) passing through them. Lagrange interpolation is an obvious generalization to this.
We first prove the existence part of this theorem. For a particular $k\leq n-1$ consider the set of $n$-coordinate pairs(we call sets with the aftermentioned property ‘special’), such that $(x_{k},1)$ belongs to the set and for all $i\leq n-1$ and $i\neq k$, $(x_{i},0)$ belongs to the set. Now we can construct the polynomial function: $$
f_{k}(x) = \frac{(x-x_0)}{(x_k-x_0)} \cdots \frac{(x-x_{k-1})}{(x_k-x_{k – 1})} \frac{(x-x_{k+1})}{(x_k-x_{k+1})} \cdots \frac{(x-x_{n-1})}{(x_j-x_{n-1})} =\prod_{0\le m\le n-1\ m\neq k} \frac{x-x_m}{x_k-x_m}$$
Clearly this function of degree $n-1$, fits the special $n$-coordinate sets for all $k$. Now given any $n$-coordinate set,$X$, for all $x$-coordinates, $x_{k}$, consider the function $f_{k}$ corresponding to the special set of $n$-coordinate pairs, such that $(x_{k},1)$ belongs to the pair. Through these $f_{k}$’s we can construct a polynomial function: $y_0f_0+y_1f_1\cdots+y_{n-1}f_{n-1}$ where $y_{m}’s$ are the $y$-coordinates of $X$ it’s easy to see that this is a $n-1$ degree polynomial function which fits $X$.
Uniqueness can be proven by algebra.