The aim of this blogpost is to prove that given $n$ points with distinct $x$ coordinates there is a unique polynomial function passing through all of them. Basically this polynomial is the (unique) polynomial of lowest degree that ‘fits’ given data. This theroem is known as the ‘Lagrange interpolation theorem’ in numerical analysis.
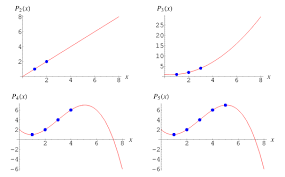
From hence forth by a set of $n$-coordinate pairs we refer to a set indexed by $0,1,\cdots,n-1$, such that the $x$-coordinates of all tuples in the set are distinct. It is well know that given a set of $2$-coordinate pairs one can find a unique linear function(a degree one polynomial) passing through them. Lagrange interpolation is an obvious generalization to this.
We first prove the existence part of this theorem. For a particular $k\leq n-1$ consider the set of $n$-coordinate pairs(we call sets with the aftermentioned property ‘special’), such that $(x_{k},1)$ belongs to the set and for all $i\leq n-1$ and $i\neq k$, $(x_{i},0)$ belongs to the set. Now we can construct the polynomial function: $$
f_{k}(x) = \frac{(x-x_0)}{(x_k-x_0)} \cdots \frac{(x-x_{k-1})}{(x_k-x_{k – 1})} \frac{(x-x_{k+1})}{(x_k-x_{k+1})} \cdots \frac{(x-x_{n-1})}{(x_j-x_{n-1})} =\prod_{0\le m\le n-1\ m\neq k} \frac{x-x_m}{x_k-x_m}$$
Clearly this function of degree $n-1$, fits the special $n$-coordinate sets for all $k$. Now given any $n$-coordinate set,$X$, for all $x$-coordinates, $x_{k}$, consider the function $f_{k}$ corresponding to the special set of $n$-coordinate pairs, such that $(x_{k},1)$ belongs to the pair. Through these $f_{k}$’s we can construct a polynomial function: $y_0f_0+y_1f_1\cdots+y_{n-1}f_{n-1}$ where $y_{m}’s$ are the $y$-coordinates of $X$ it’s easy to see that this is a $n-1$ degree polynomial function which fits $X$.
Uniqueness can be proven by algebra.
bx1v8b
ΠΠ»Π΅Π³Π°Π½ΡΠ½ΠΎΡΡΡ ΠΈ ΡΡΠΈΠ»Ρ Π² ΠΊΠ°ΠΆΠ΄ΠΎΠΉ Π΄Π΅ΡΠ°Π»ΠΈ.
ΠΠ΅Π±Π΅Π»Ρ ΠΏΡΠ΅ΠΌΠΈΡΠΌ https://byfurniture.by .
ΠΠ΄Π΅ΠΈ Π΄Π»Ρ ΠΎΡΠΎΡΠΌΠ»Π΅Π½ΠΈΡ Π΄ΠΈΠ·Π°ΠΉΠ½Π΅ΡΡΠΊΠΎΠΉ ΠΌΠ΅Π±Π΅Π»ΡΡ.
ΠΠΈΠ·Π°ΠΉΠ½Π΅ΡΡΠΊΠ°Ρ ΠΌΠ΅Π±Π΅Π»Ρ ΠΏΡΠ΅ΠΌΠΈΡΠΌ-ΠΊΠ»Π°ΡΡΠ° https://byfurniture.by .
https://honda-fit.ru/forums/index.php?autocom=gallery&req=si&img=7034
Π’ΠΎΠΏ Π½Π°ΠΏΡΠ°Π²Π»Π΅Π½ΠΈΡ Π΄Π»Ρ ΠΎΡΠ΄ΡΡ Π° Π² ΡΡΠΎΠΏΠΈΠΊΠ°Ρ .
ΠΠΊΠ·ΠΎΡΠΈΡΠ½ΠΈ ΠΏΠΎΡΠΈΠ²ΠΊΠΈ ΠΠΊΠ·ΠΎΡΠΈΡΠ½ΠΈ ΠΏΠΎΡΠΈΠ²ΠΊΠΈ .
ΠΠ±Π·ΠΎΡΡ ΠΏΠΎΠΏΡΠ»ΡΡΠ½ΡΡ Π°Π½ΡΠΈΡΡΡΠ΅ΡΡ ΠΈΠ³ΡΡΡΠ΅ΠΊ.
ΠΠ½ΡΠΈΡΡΡΠ΅Ρ ΡΠΈΠ΄ΠΆΠ΅Ρ ΠΈΠ³ΡΠ°ΡΠΊΠΈ https://www.antistres-igrachki.com/ .
ΠΡΠΊΠ»Ρ Π±Π΅Π±Π΅ΡΠ° β Π»ΡΡΡΠΈΠ΅ Π΄ΡΡΠ·ΡΡ Π²Π°ΡΠ΅Π³ΠΎ ΡΠ΅Π±Π΅Π½ΠΊΠ°.
ΠΠ΅ΠΊΠΈ ΠΊΡΠΊΠ»ΠΈ Π±Π΅Π±Π΅ΡΠ° http://www.kukli-bebeta.com/ .
ΠΠ½Π½ΠΎΠ²Π°ΡΠΈΠΎΠ½Π½ΡΠ΅ ΡΠ΅ΡΠ΅Π½ΠΈΡ Π΄Π»Ρ ΠΈΠΌΠΏΠ»Π°Π½ΡΠ°ΡΠΈΠΈ Π½Π° 4 ΠΈΠΌΠΏΠ»Π°Π½ΡΠ°Ρ .
ΠΠΌΠΏΠ»Π°Π½ΡΠ°ΡΠΈΡ 4 all ΠΏΠΎΠ΄ ΠΊΠ»ΡΡ http://www.belfamilydent.ru/services/implantaciya-allon4 .
ΠΡΠ΅ΠΈΠΌΡΡΠ΅ΡΡΠ²Π° Π·ΡΠ±Π½ΡΡ ΠΌΠΎΡΡΠΎΠ² ΠΏΠ΅ΡΠ΅Π΄ ΠΈΠΌΠΏΠ»Π°Π½ΡΠ°ΠΌΠΈ.
Π‘ΠΊΠΎΠ»ΡΠΊΠΎ ΡΡΠΎΠΈΡ ΠΌΠΎΡΡΠΎΠ²ΠΈΠ΄Π½ΡΠΉ ΠΏΡΠΎΡΠ΅Π· koronki-blog.ru/mostovidnoe-protezirovanie .
ΠΡΠΎΠ±Π΅Π½Π½ΠΎΡΡΠΈ ΡΡ ΠΎΠ΄Π° Π·Π° ΠΌΠΎΡΡΠΎΠ²ΠΈΠ΄Π½ΡΠΌΠΈ Π½Π΅ΡΡΠ΅ΠΌΠ½ΡΠΌΠΈ ΠΏΡΠΎΡΠ΅Π·Π°ΠΌΠΈ.
ΠΠΎΡΡΠΎΠ²ΠΈΠ΄Π½ΡΠΉ ΠΏΡΠΎΡΠ΅Π· Π½Π° Π²Π΅ΡΡ Π½ΡΡ ΡΠ΅Π»ΡΡΡΡ http://belfamilydent.ru/services/mostovidnoe-protezirovanie/ .
Π‘ΠΎΠ²ΡΠ΅ΠΌΠ΅Π½Π½ΡΠ΅ ΠΌΠ΅ΡΠΎΠ΄Ρ SEO.
Π Π°ΡΠΊΡΡΡΠΊΠ° ΡΠ°ΠΉΡΠΎΠ² ΡΠ°ΡΡΠ½ΡΠΉ ΠΌΠ°ΡΡΠ΅Ρ Π Π°ΡΠΊΡΡΡΠΊΠ° ΡΠ°ΠΉΡΠΎΠ² ΡΠ°ΡΡΠ½ΡΠΉ ΠΌΠ°ΡΡΠ΅Ρ .
ΠΠ°ΠΊ ΡΠ΄Π΅Π»Π°ΡΡ ΠΈΠ½ΡΠ΅ΡΡΠ΅Ρ ΡΡΠΎΠ½ΡΠ΅Π½Π½ΡΠΌ Ρ ΠΏΠΎΠΌΠΎΡΡΡ Π΄ΠΈΠ·Π°ΠΉΠ½Π΅ΡΡΠΊΠΈΡ ΡΠ»Π΅ΠΌΠ΅Π½ΡΠΎΠ².
ΠΠΈΠ·Π°ΠΉΠ½Π΅ΡΡΠΊΠ°Ρ ΠΌΠ΅Π±Π΅Π»Ρ ΠΏΡΠ΅ΠΌΠΈΡΠΌ-ΠΊΠ»Π°ΡΡΠ° http://www.byfurniture.by .
ΠΡΠΎΡΠ΅ΡΡΠΈΠΎΠ½Π°Π»ΡΠ½ΡΠΉ ΡΠ»Π΅ΠΊΡΡΠΈΠΊ Π½Π΅Π΄ΠΎΡΠΎΠ³ΠΎ Π² ΠΠΎΡΠΊΠ²Π΅
ΠΡΠ·Π²Π°ΡΡ ΡΠ»Π΅ΠΊΡΡΠΈΠΊΠ° Π½Π° Π΄ΠΎΠΌ https://elektrik-master-msk.ru .
Π‘ΠΎΠ²Π΅ΡΡ ΠΏΠΎ SEO Π΄Π»Ρ Π½Π°ΡΠΈΠ½Π°ΡΡΠΈΡ , Ρ ΠΌΠΈΠ½ΠΈΠΌΠ°Π»ΡΠ½ΡΠΌΠΈ Π·Π°ΡΡΠ°ΡΠ°ΠΌΠΈ.
GSA ser http://kwork.ru/links/41629912/seo-pushka-dlya-sayta-mnogourovnevaya-piramida-ssylok-pod-klyuch/ .
Π£ Π½Π°Ρ Π΅ΡΡΡ Π²ΡΡ Π΄Π»Ρ ΠΈΠ΄Π΅Π°Π»ΡΠ½ΠΎΠ³ΠΎ ΠΏΡΠ°Π·Π΄Π½ΠΈΠΊΠ°, ΠΏΠΎ Π²ΡΠ³ΠΎΠ΄Π½ΡΠΌ ΡΠ΅Π½Π°ΠΌ.
ΠΠ΅Π»ΠΈΠ΅Π²ΡΠ΅ ΡΠ°ΡΠΈΠΊΠΈ Ρ Π΄ΠΎΡΡΠ°Π²ΠΊΠΎΠΉ ΠΠΈΠΆΠ½ΠΈΠΉ ΠΠΎΠ²Π³ΠΎΡΠΎΠ΄ https://shariki-shop47.ru .
ΠΠ°ΠΊΠ°Π·Π°ΡΡ ΡΠ²Π΅ΡΡ Ρ Π΄ΠΎΡΡΠ°Π²ΠΊΠΎΠΉ Π² ΠΠΎΡΠΊΠ²Π΅
ΠΠΎΡΡΠ°Π²ΠΊΠ° ΡΠ²Π΅ΡΠΎΠ² Π² ΠΠΎΡΠΊΠ²Π΅ β ΡΡΠΎ ΡΠ΄ΠΎΠ±Π½ΡΠΉ ΡΠΏΠΎΡΠΎΠ± ΠΏΠΎΡΠ°Π΄ΠΎΠ²Π°ΡΡ Π±Π»ΠΈΠ·ΠΊΠΈΡ . ΠΡΠ±ΠΎΡ ΡΠ΅ΡΠ²ΠΈΡΠΎΠ² ΠΏΠΎ Π΄ΠΎΡΡΠ°Π²ΠΊΠ΅ ΡΠ²Π΅ΡΠΎΠ² Π² ΠΠΎΡΠΊΠ²Π΅ ΠΏΡΠΎΡΡΠΎ ΠΎΠ³ΡΠΎΠΌΠ΅Π½, ΡΡΠΎ ΠΏΠΎΠ·Π²ΠΎΠ»ΡΠ΅Ρ Π½Π°ΠΉΡΠΈ ΠΈΠ΄Π΅Π°Π»ΡΠ½ΡΠΉ Π²Π°ΡΠΈΠ°Π½Ρ.
ΠΠ΅ΡΠ΅Π΄ ΡΠ΅ΠΌ ΠΊΠ°ΠΊ ΡΠ΄Π΅Π»Π°ΡΡ Π·Π°ΠΊΠ°Π·, ΡΡΠΎΠΈΡ ΠΎΠΏΡΠ΅Π΄Π΅Π»ΠΈΡΡΡΡ Ρ Π±ΡΠΊΠ΅ΡΠΎΠΌ. Π Π΅ΠΊΠΎΠΌΠ΅Π½Π΄ΡΠ΅ΡΡΡ ΡΠ°ΡΡΠΌΠΎΡΡΠ΅ΡΡ ΠΊΠ°ΠΊ ΡΡΠ°Π½Π΄Π°ΡΡΠ½ΡΠ΅ Π²Π°ΡΠΈΠ°Π½ΡΡ, ΡΠ°ΠΊ ΠΈ Π±ΠΎΠ»Π΅Π΅ ΠΊΡΠ΅Π°ΡΠΈΠ²Π½ΡΠ΅ ΡΠ΅ΡΠ΅Π½ΠΈΡ.
ΠΠ΅ Π·Π°Π±ΡΠ²Π°ΠΉΡΠ΅ ΠΏΡΠΎΠ²Π΅ΡΡΡΡ ΡΡΠΎΠΊΠΈ Π΄ΠΎΡΡΠ°Π²ΠΊΠΈ ΠΈ Π΄ΠΎΠΏΠΎΠ»Π½ΠΈΡΠ΅Π»ΡΠ½ΡΠ΅ ΠΎΠΏΡΠΈΠΈ, ΠΊΠΎΡΠΎΡΡΠ΅ ΠΌΠΎΠ³ΡΡ ΠΏΡΠ΅Π΄Π»ΠΎΠΆΠΈΡΡ ΡΠ΅ΡΠ²ΠΈΡΡ. Π Π½Π΅ΠΊΠΎΡΠΎΡΡΡ ΠΊΠΎΠΌΠΏΠ°Π½ΠΈΡΡ Π²Ρ ΠΌΠΎΠΆΠ΅ΡΠ΅ Π΄ΠΎΠ±Π°Π²ΠΈΡΡ ΠΊ ΡΠ²ΠΎΠ΅ΠΌΡ Π·Π°ΠΊΠ°Π·Ρ ΠΎΡΠΊΡΡΡΠΊΡ ΠΈΠ»ΠΈ Π΄ΠΎΠΏΠΎΠ»Π½ΠΈΡΠ΅Π»ΡΠ½ΡΠ΅ Π½Π΅Π±ΠΎΠ»ΡΡΠΈΠ΅ ΠΏΡΠ΅Π·Π΅Π½ΡΡ.
ΠΡΠ±ΠΈΡΠ°ΠΉΡΠ΅ ΠΏΡΠΎΠ²Π΅ΡΠ΅Π½Π½ΡΠ΅ ΡΠ΅ΡΠ²ΠΈΡΡ Ρ Ρ ΠΎΡΠΎΡΠΈΠΌΠΈ ΠΎΡΠ·ΡΠ²Π°ΠΌΠΈ ΠΈ ΡΠ΅ΠΏΡΡΠ°ΡΠΈΠ΅ΠΉ. Π’Π°ΠΊΠΎΠΉ ΠΏΠΎΠ΄Ρ ΠΎΠ΄ ΠΈΡΠΊΠ»ΡΡΠΈΡ Π½Π΅ΠΏΡΠΈΡΡΠ½ΡΠ΅ ΡΠΈΡΡΠ°ΡΠΈΠΈ Ρ ΠΊΠ°ΡΠ΅ΡΡΠ²ΠΎΠΌ ΡΠ²Π΅ΡΠΎΠ² ΠΈ ΡΡΠΎΠΊΠ°ΠΌΠΈ Π΄ΠΎΡΡΠ°Π²ΠΊΠΈ.